A Machine Learning Approach to Mass-Conserving Ice Thickness Interpolation

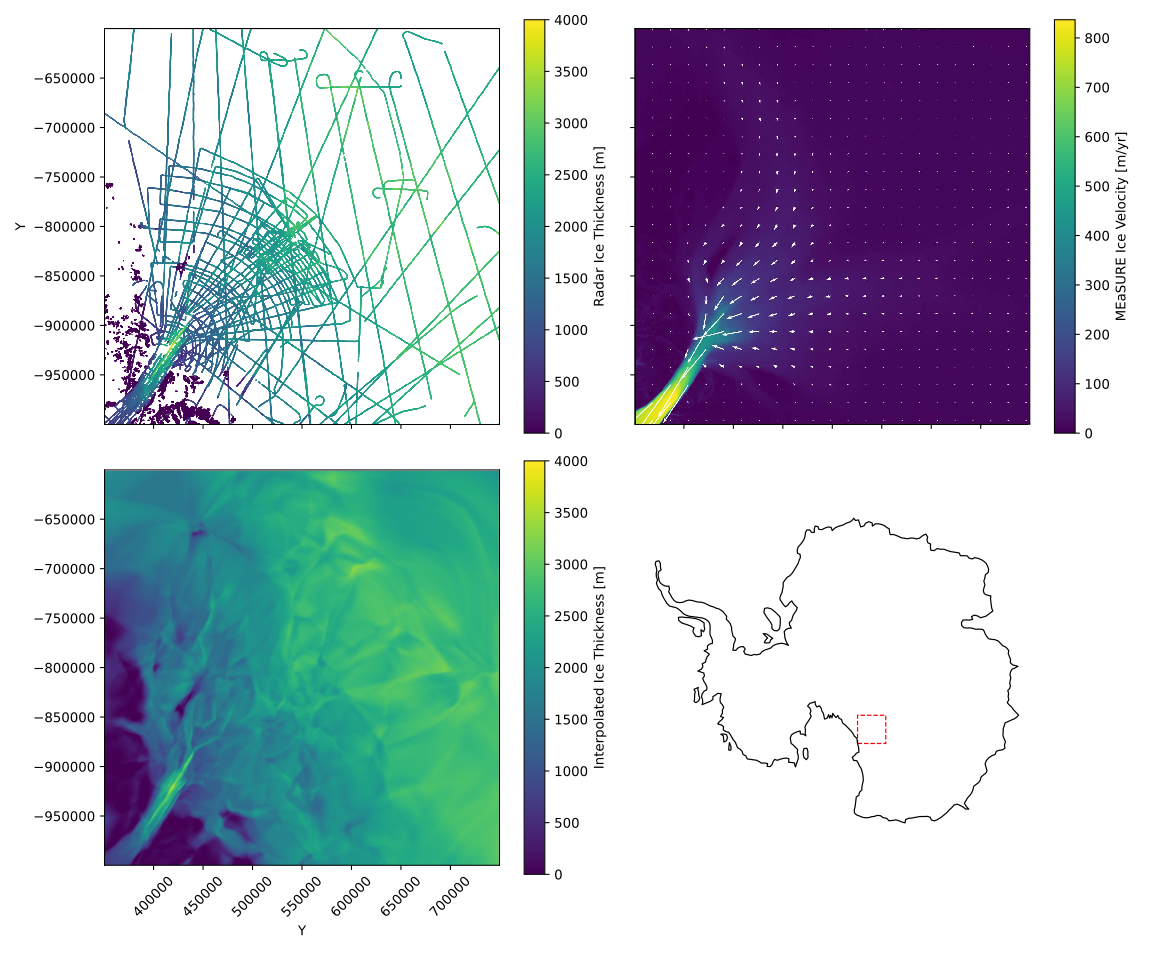
Knowing the topography of the bed under Earth’s ice sheets and glaciers is critical to predicting how the ice will evolve over time, but this topographic information is hidden by the ice itself. The most wide-scale measurements of ice thickness, and, thus, the subglacial topography, come from airborne ice-penetrating radar instruments. These instruments, operating at low frequencies, can penetrate through the ice to measure ice thicknesses of up to several kilometers. These measurements, however, are only sparesly available throughout Antarctica. As a result, most ice sheet models use interpolated maps of the bed, made by filling in the gaps in these sparse measurements.

One approach to filling in these gaps is to use a physics-based approach based on the conservation of mass. Given a known ice velocity and thickness at one position, the downstream thickness can then be inferred only based on the velocity at the downstream location. Although uncertainties still exist, this method has proven effective at producing high-quality interpolated bed maps in fast-flowing regions of Antarctica and Greenland.

Here we explore the use of a physics-informed neural network to perform this interpolation. A small feed-forward neural network takes coordinates as an input and predicts the ice thickness and velocity at that location. The loss function is augmented with a physics-based term that penalizes deviations from the residual form of the mass conservation PDE.

This approaches uses surface velocity measurements and sparse radar-based ice thickness measurements to create a map of the subglacial topography.

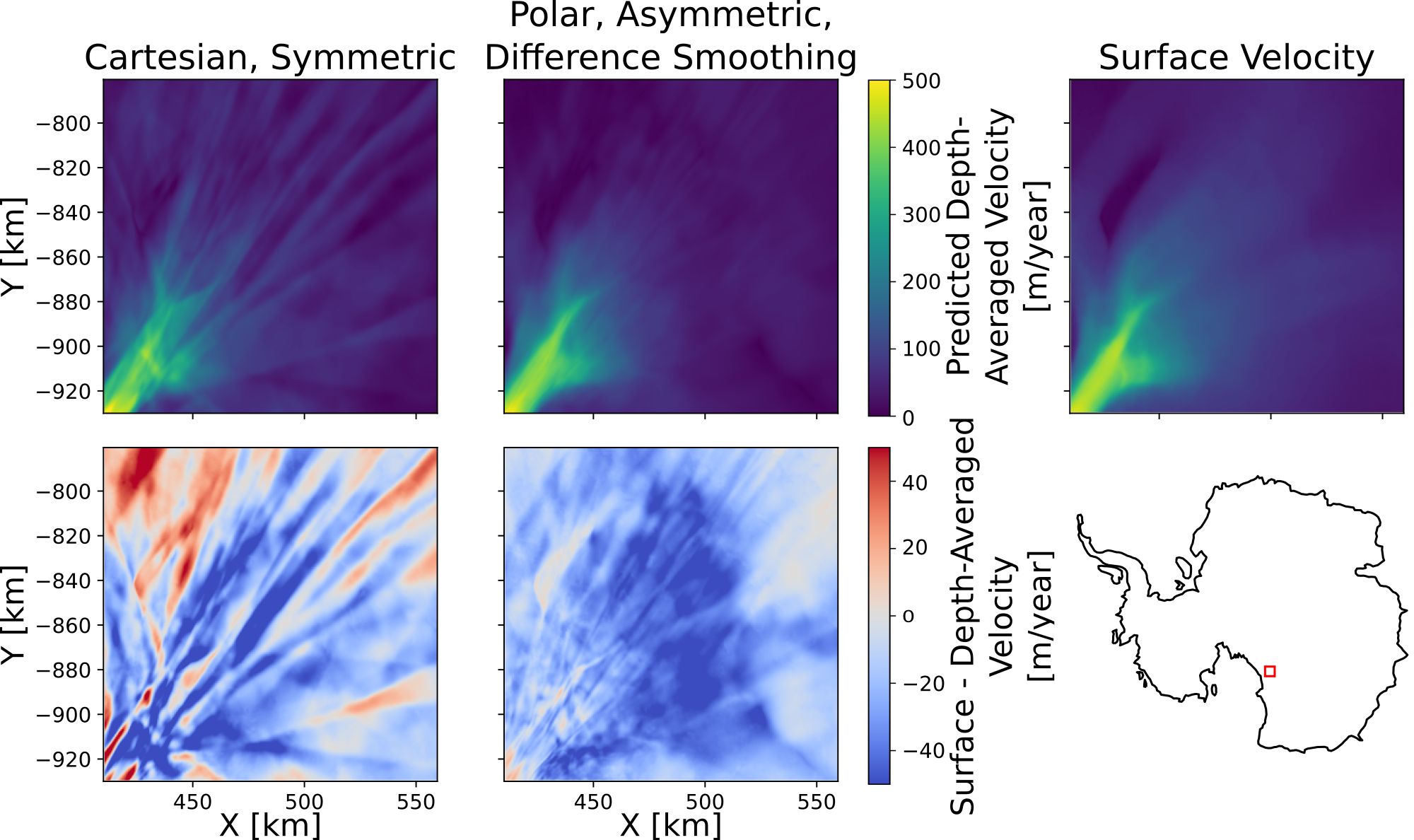
Using a physics-informed neural network to solve this problem allows for the flexible incorporation of different constraints and regularizations into this undefined inverse problem. One of the challenges with mass conservation-based approaches is that only the surface velocity is known in most cases, not the depth-averaged velocity. One approach is to simply enforce that the depth-averaged velocity must be within some limit of the surface velocity, however this can produce unrealistic patterns in the differences between the surface and depth-averaged velocity. We demonstrate applying a smoothing term to penalize sharp changes in the difference between the surface and depth-averaged velocity. This discourages sharp changes in the depth-averged velocity unless there is evidence for this sharp transition in the surface velocity data.

Our results in the test region are similar to BedMachine Antarctica, the current state-of-the-art ice thickness map. Both our work and BedMachine Antarctica use the same concept of mass conservation interpolation in this area, however we apply a completley different method of solving this optimization problem. The similarity of the results suggests that physics-informed neural networks are a viable approach to solving this optimization problem while introducing more flexibility in the constraints and regularizations that can be applied.